How computers can help us understand word meanings as they change over time

Calling someone nice was once an insult ¹. Coming from the Latin nescius, meaning ignorant, it was synonymous with foolish and simple-minded in the 13th century. Then, over hundreds of years, it underwent a dramatic transformation ("foolish" → "fussy" → "dainty" → "precise" → "agreeable" → "kind") to reach its modern meaning.

Semantics /səˈman(t)iks/ is the study of meaning in language.

This kind of change is not unusual. Languages are dynamic. Words travel across centuries, genres, and communities. They appear in religious, legal, scientific, musical, and casual (to name a few) contexts. Therefore, they evolve as their usage changes (often from humans and culture changing). In linguistics, this phenomenon is known as semantic drift or semantic change.

Just take a look at slang (especially in online language). The word cool once only meant moderately cold, but now also means something like interesting or stylish. To ghost someone is not to turn them into a specter, but rather to ignore their texts.

Ok, how do we study / measure / quantify semantic drift? Well, traditional philology can detect such changes through meticulous reading and documentation, but this approach is necessarily limited in scale. The sheer magnitude of texts (not to mention the words themselves) makes manual analysis incredibly time-consuming, far exceeding the capacity of an individual researcher.

To approach this problem, we first need to understand what meaning is (or if that's too philosophical for you - we have to figure out how meaning is constructed).

The meaning of meaning

You don’t need a dictionary to sense when a word is out of place. If someone calls you nice, you (hopefully) would not take it as an insult.

This intuition comes from experience - we hear and see words used in thousands of situations and are able to slowly construct internal models of meaning.

"You shall know a word by the company it keeps." - John Firth

Simply put, this says that you can deduce the meaning of a word by looking at the words around it (its context). This is the basis of distributional semantics, deriving the distributional hypothesis:

Words that occur in similar contexts tend to have similar meanings.

Since meaning is reflected in context, we should create representations of each word based on the contexts in which it appears.

With direction and magnitude

Turns out, computers can help us build such representations by encoding surrounding context words into numeric vectors.

Word embedding models represent each word as a vector (think long list of numbers) in a high-dimensional space. These vectors are not assigned by hand. Instead, they are learned from large amounts of text by observing how words are used. The core principle is still the same distributional hypothesis proposed by linguists decades ago.

Early approaches counted word co-occurrences (how often each word appears next to each other word) and stored them in large matrices to construct the vectors. A stronger strategy, leveraged by modern models, is to have a small neural network learn word representations automatically by solving a prediction task. To make good predictions, the model must learn meaningful vectors that capture relationships between words.

Word2Vec ², introduced in 2013, popularized two inverse training strategies: Continuous Bag of Words (CBOW) and Skip-gram.

Fill in the ____

CBOW hides a word in a sentence and asks the model to guess it from the surrounding words.

May the ____ be with you. (hint: Star Wars)

The model uses the nearby words (contained in a set window size) to predict the missing target word. If I remove the word 'the', you can see how the predicted word changes.

May ____ be with you.

Here, instead of 'force', peace or god or happiness come to mind. So, words that could fill the same blank end up with similar vector representations.

Skip-gram is basically the inverse. Instead of guessing a word from its context, it uses a word to guess its neighbors.

Given the word tennis, the model learns that words like court, racket, ball, or player often appear nearby. During training, words that produce similar contexts are grouped closer together in the embedding space; words used differently are farther apart.

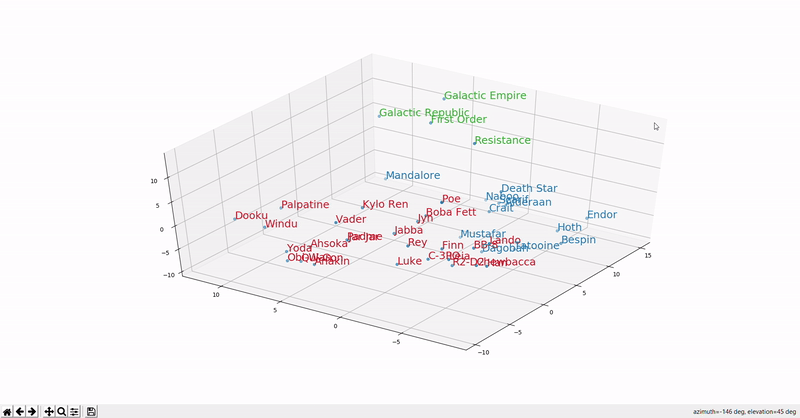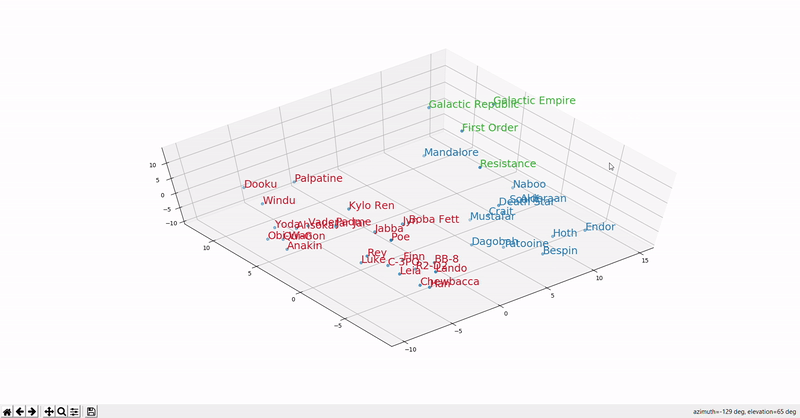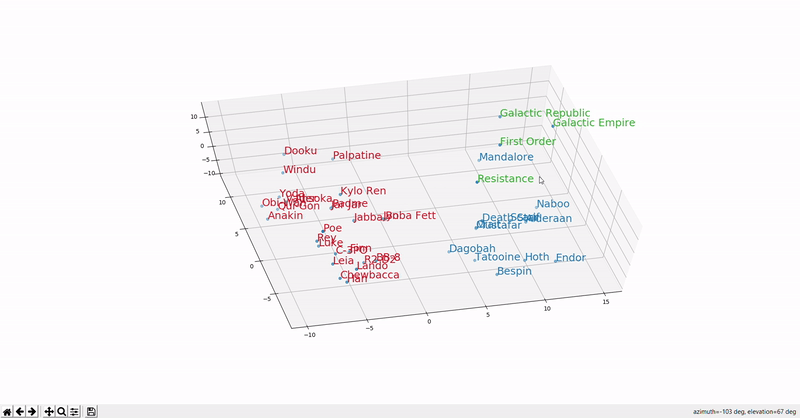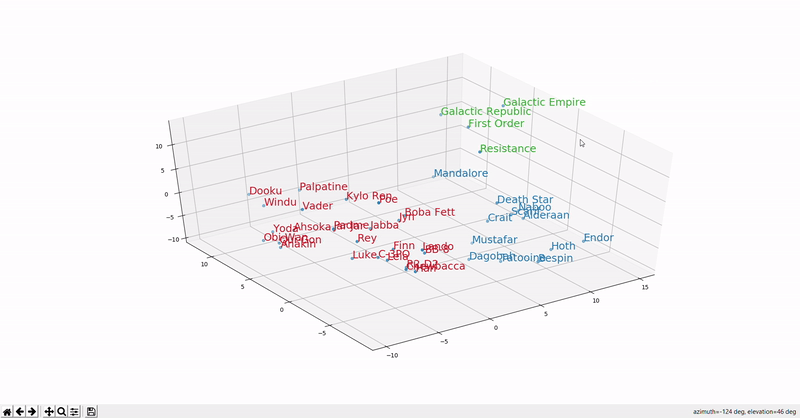Continuing the Star Wars theme, this GIF (source) shows the distribution of Star Wars word embeddings. Words of the same type (characters, places, organizations) are clustered together.

Analogies

A very cool (not temperature) property of word embeddings is that they can solve analogies. The most famous example is:

king - man + woman ≈ queen

If you remove the 'man' part from king, you'll get something like ruler. Then, if you add 'woman' to that, you get queen.

More of a side thought: the meanings of man and woman are also changing with contemporary usage, which is an interesting case of semantic drift.

Comparison is the thief of joy

So, we have all these vectors that represent the meanings of words in some high-dimensional space (for reference, DeepSeek-V3's dimensionality is 7168 ³). It's hard to comprehend this space (really, anything above 3D is difficult), but don't panic yet.

We can use properties of vectors to compare two words to each other and see how similar they are. The most common measure is cosine similarity, which is the dot product of the two vectors divided by the product of their magnitudes. Without getting too much into the math, this helps us assign similarity scores (-1 to 1) to a pair of words based on the angle between them (ignoring the length of the vectors).

For those who already forgot,

1. Semantic drift describes how the meaning of a word changes over time.
2. The context around a word reflects the meaning of the word.
3. This idea is used to train word embeddings, which are numeric representations of words.
4. Similar words are closer together in the embedding space and have higher cosine similarity scores.

I highly recommend that you check out this quick video by @3Blue1Brown to visualize these concepts!

Tying it together

How does all of this word embeddings stuff apply to semantic drift?

Let's go back to our original question: how can we study, measure, or quantify semantic drift? Word embeddings provide a powerful and scalable way to do so. Unlike traditional methods, which involve painstaking manual reading, embeddings let us quantify meaning mathematically and track how it shifts over time.

We can construct multiple vector spaces of word embeddings from different periods of time, and then compare vectors of the same word across different periods to measure change. This methodology was introduced by Hamilton et al. in their 2016 paper ⁴.

There are two main ways to compare vectors here:

1. Global Measure: This measures how much a word has changed in the overall semantic space using the cosine similarity between its vectors from two different time periods. A low similarity score indicates that the word's meaning has shifted a lot.
2. Local Neighborhood Measure: This measures changes in a word's k-nearest neighbors. For example, nice in the 12th century would have neighbors like stupid and foolish, while in the 21st century, it would be closest to kind and gentle.

Case Study

With these tools in hand, I embarked on a research project to apply word embeddings to study semantic drift in ancient Sanskrit texts to see if this methodology could be applied successfully to languages other than English.

I defined the time periods by grouping digitally available texts into the following eras:

1. Vedic (1500-500 BCE)
2. Early Classical Upaniṣadic (700-200 BCE)
3. Epics (400 BCE - 400 CE)
4. Śāstra + Sūtra (200 BCE - 500 CE)

Like described before, for each period, I create a vector space of word embeddings then compare the vectors across different periods to measure semantic drift. My main research question is: Can diachronic word embeddings capture measurable semantic shift in Sanskrit words across ancient texts? And how do these changes compare with known / hypothesized word changes in Sanskrit linguistic literature?

However, I found very quickly during my research that Sanskrit poses unique challenges for this task. First, Sanskrit has a feature known as Sandhi (phonological fusion). Words often merge at boundaries and create new, fused forms, which disrupt semantic information and increase sparsity (the total number of unique "words" skyrockets).

Furthermore, Sanskrit exhibits extensive compounding (samāsa), where multiple words are combined into a single grammatical unit that expresses a new meaning. For refrence, here are some fixed compounds in modern languages:

1. toothbrush: English, literally "brush for teeth"
2. rompecabezas: Spanish, means 'puzzle': but literally "head-breakers," because solving it is so hard for the brain

Sanskrit compounds are this but on steroids: they are much longer, highly productive (speakers can create a potentially unlimited number of new words), and context-dependent. To a computational model, these constructions appear as rare, atomic tokens, even though they contain several meaningful components, making it difficult to recover shared semantic structure from raw surface text.

Take a look at this 42 character long "word" that I found in the corpus:

grahaṇasvarūpāsmitānvayārthavattvasaṃyamād

We don't want to treat such forms as individual tokens, as it severely degrades the quality of learned word representations. Thankfully, there are tools to handle this, but the far most robust (and beautifully integrated with Python) is ByT5-Sanskrit ⁵. It provides a pre-trained neural network that can pretty accurately split Sandhi and compound forms. Our word is now split into:

grahaṇa sva rūpa asmitā anvaya arthavattva saṃyamāt

Second, Sanskrit is a highly inflected language. Nouns can have over 70 forms, and verbs up to 900 forms. We don't want this immense morphological variation to cause forms of the same root word to be treated as separate tokens. Morphologically rich languages have significant grammatical information (like tense, number, case, gender) packed within the words themselves, often adding morphemes to words to express more meaning.

To clear this noise, I used lemmatization to reduce words to their base, or canonical, form. This is basically like converting 'running', 'runs', 'ran' all to 'run'.

Next, Sanskrit contains lots of polysemous words, meaning each word can have multiple meanings based on the context. A famous example in English is bank, which can mean a financial institution or the edge of a river. To address this issue, I am looking into contextualized embeddings, which are dynamic vector representations of words that change based on surrounding context. Here, models like BERT or GPT generate a new embedding for each token every time it appears, based on the entire input sequence.

Another interesting aspect is that Sanskrit has a free word order, due to its highly inflected nature. You can basically switch around the words like Yoda (too many Star Wars references?) in a sentence and it would still retain its meaning.

There's also different models that can be used to generate embeddings. Word2vec and BERT, mentioned earlier, are key examples. fastText is an extension of Word2vec that uses character n-grams (e.g. 'apple' becomes [ap, app, ppl, ple, le]) to represent words. It basically operates at the sub-word level, which can be helpful for languages like Sanskrit that have extensive morphology ⁶.

I'm currently in the process of training models with different configurations to evaluate which techniques are most effective for Sanskrit. If you're interested, check out my other blog posts for more details about this project or me.

Conclusion

Thanks for reading! I'd love to hear your thoughts, suggestions, and questions - please do reach out.